Použití Constraints v dynamických blocích – 1. díl - průběh posouvacích sil
Kategorie » téma: AutoCAD
16.04.2009 00.24 | | Komentáře: 0 komentářů | Přečteno: 13113x
V předešlých příspěvcích věnovaných Constraints jsme se zabývali jejich použitím přímo v modelovém prostoru. V následujícím příkladu si předvedeme, jakým způsobem použít Constraints v dynamických blocích. Funkčnost si ukážeme opět na prostém nosníku, ale tentokrát zatíženém spojitým rovnoměrným zatížením a osamělým břemenem.
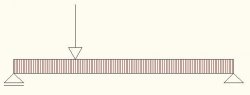
| Nejprve si v modelovém prostoru nakreslíme schéma prostého nosníku s podporami, spojitým zatížením a osamělým břemenem. Spojité zatížení doporučuji volit jako obdélník, který se vyšrafuje pomocí asociativních šraf výběrem objektu. Tím zajistíme vyšrafování spojitého zatížení i při změně délky nosníku. |
| ||||
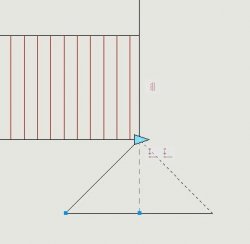
| Z nosníku vytvoříme blok a v editoru bloků začneme přidávat Constraints. Nejprve přidáme Linear Constraint ke spodní vodorovné hraně reprezentující nosník. Aby se s nosníkem protahovalo i spojité zatížení stačí přidat Vertical Constraint ke krajním svislým hranám zatížení. K levému krajnímu bodu nosníku vložíme Fix Constraint. Tato podpora bude zůstávat na místě a manipulovat se bude pouze s podporou vpravo. Pravou podporu připojíme k nosníku pomocí Coincident Constraint. Abychom zajistily, že se bude pohybovat i spodní vodorovná hrana podpory vytvoříme si pomocnou čáru směřující od vrcholu podpory ke středu spodní hrany podpory a svážeme ji s vrchem a středem spodní hrany podpory opět pomocí Coincident Constraint. |
| ||||
| Jestliže nebudeme chtít, aby se svislá pomocná čára zobrazovala po vložení hotového bloku, převedeme ji na Construction Geometry pomocí stejnojmenné ikony vlevo od ikony Parameters Manager. Po klepnutí na tuto ikonu a výběru čáry, kterou chceme převést budeme dotázáni, zda chceme čáru konvertovat na pomocnou, nebo zpět z pomocné na normální (Convert / Revert). Pomocí tohoto příkazu se dá tedy pomocná geometrie převádět i zpět. |
| ||||
| Další Linear Constraint vložíme mezi levou podporu nosníku a osamělé břemeno. Aby šipka reprezentující osamělé břemeno zůstala svislá, přidáme k čáře Vertical Constraint. Šipku k čáře připojíme pomocí pomocné čáry podobně jako u pravé podpory s tím rozdílem, že zde ještě pomocí Vertical Constraint zajistíme, aby pomocná čára zůstala při manipulaci s břemenem svislá. |
| ||||
| Pro lepší identifikaci podpor označíme levou podporu písmenem A pravou písmenem B. Písmeno A nemusíme k podpoře nijak kotvit, protože tato podpora zůstává na místě. U podpory B je tomu již jinak – levá podpora je v pohybu. Vyneseme si tedy čáru například od pravého kraje značky podpory a k jejímu spodnímu bodu napíšeme písmeno B. Písmeno B přichytíme ke koncovému bodu pomocí Coincident Constraint a stejný Constraint použijeme i pro horní bod čáry a pravý bod značky podpory. Aby čára zůstávala svislá přidáme k ní Vertical Constraint a čáru převedeme pomocí Construction Geometry na pomocnou. |
| ||||
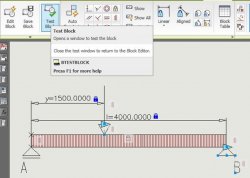
| Funkčnost bloku můžeme vyzkoušet v novém okně Test Block ještě před tím, než blok uložíme a vrátíme se do modelového prostoru. Zpět se vrátíme klepnutím na ikonu Close Test Block. |
| ||||
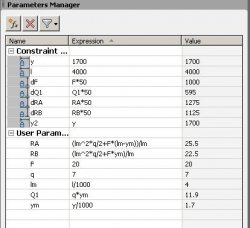
| V následující bloku přidáme uživatelské parametry, kterými zadáme hodnotu spojitého rovnoměrného zatížení (q) a hodnotu osamělého břemene (F) a spočítáme reakce v podporách (RA a RB). Abychom nemuseli ve vzorcích stále používat dělení tisícem z důvody převodu milimetrů na metry, zavedeme si dvě nové proměnné a to sice lm=l/1000 a ym = y/1000. |
| ||||
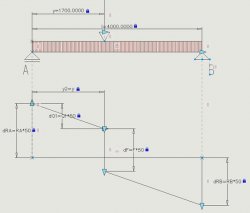
| Nyní si pomocí polyline nakreslíme přibližně průběh posouvacích sil, tak jak bude vypadat. K průběhu přidáme čáry, které později převedeme na pomocné a které nám zajistí, aby se obrazec posouvacích sil pohyboval s měnící se délkou nosníku. K těm čarám, které budou vždy svislé přidáme Vertical Constraint (to se týká obou reakcí a svislé čáry pod osamělým břemenem). Vertical Constraint ovšem přidáme i k pomocným čarám směřujícím svisle od nosníku k obrazci posouvacích sil. K vodorovné ose přidáme Horizontal Constraint. Navazující čáry k sobě svážeme pomocí Coincident Constraint. Délka levé svislé čáry obrazce bude odpovídat velikosti reakce v podpoře A. Délka pravé svislé čáry obrazce bude odpovídat velikosti reakce v podpoře B. Délka svislé čáry pod osamělým břemenem bude odpovídat hodnotě osamělého břemene. Pokles posouvacích sil mezi Levou podporou a osamělým břemenem, které se od levé podpory nachází ve vzdálenosti y je Ra-y*q. To je vše co potřebujeme k tomu, abychom obrazec “okótovali” dynamickými Constraints. Protože vynesení hodnot posouvacích sil ve velikosti, kde by 1 kN odpovídal 1 jednotce ve výkresu by bylo nepřehledné, budeme hodnoty posouvacích sil násobit padesáti. Proto jsou do Parameters Manageru přidány další parametry: dRa = RA*50 dRB = RB*50 dF = F*50 Hodnotu posouvací síly u osamělého břemene označíme jako Q1 = q*ym a stejně jako v předchozích případech dQ1 = Q1*50 Vzdálenost osamělého břemene od levé podpory označíme jako y2. Hodnota y2 odpovídá vzdálenosti y y2=y |
| ||||
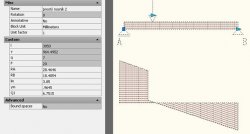
| Tímto je dostatečně definován obrazec posouvacích sil. Po vyšrafování asociativními šrafami a uložení bloku můžeme vyzkoušet jeho funkčnost. Délku nosníku a polohu osamělého břemene volíme graficky pomocí uzlů, nebo číselně zadáním hodnoty v panelu Properties. Hodnota spojitého rovnoměrného zatížení a osamělého břemene lze zadat pouze číselně v dialogu Properties. Pokud nechceme, aby se v panelu Properties zobrazovali po vybrání bloku parametry typu dRA, dRAB, dF, dQ1, které slouží pouze pro vykreslení obrazce, vybereme v editoru bloků tyto parametry a v dialogu Properties zadáme u vlastnosti Show Properties hodnotu No |
| ||||
|
| ||||
| Tyto obrázky ilustrují chování bloku a přepočet reakcí při změně jeho parametrů. Na posledním obrázku je vidět průběh posouvacích sil v případě, že osamělému břemenu zadáme nulovou hodnotu. |
|
Komentáře:
Tento článek zatím neobsahuje žádné komentáře.